Stata Regression Models

Topics

  • Models with continuous outcomes
    • OLS regression
    • OLS model assumptions and diagnostics
    • Including interaction terms
    • Including categorical predictors
  • Models with binary outcomes
    • Logistic regression
    • Obtaining odds ratios
  • Exporting & saving results
    • Regression tables
    • Model comparison
  • Obtaining quantities of interest
    • Margins of responses
      • APM: Average Predictive Margins
      • PMM: Predictive Margins at the Means
      • PMR: Predictive Margins at Representative values
    • Margins of changes in responses
      • AME: Average Marginal Effects
      • MEM: Marginal Effects at the Means
      • MER: Marginal Effects at Representative values

Setup

Software and Materials

Follow the Stata Installation instructions and ensure that you can successfully start Stata.

Class structure and organization

  • Informal — Ask questions at any time. Really!
  • Collaboration is encouraged - please spend a minute introducing yourself to your neighbors!
  • If you are using a laptop, you will need to adjust file paths accordingly
  • Make comments in your do-file - save on flash drive or email to yourself

Prerequisites

This is an intermediate-level Stata modeling workshop

  • Assumes basic knowledge of Stata
  • Not appropriate for people already well familiar with modeling in Stata
  • If you are catching on before the rest of the class, experiment with command features described in help files

Goals

We will learn about the Stata modeling ecosystem by analyzing data from three datasets. In particular, our goals are to learn about:

  1. Modeling workflow
  2. Modeling continuous outcomes
  3. Modeling binary outcomes
  4. Producing regression tables
  5. Obtaining margins of responses
  6. Obtaining margins of changes in responses

Modeling workflow

Before we delve into the details of how to fit models in Stata, it’s worth taking a step back and thinking more broadly about the components of the modeling process. These can roughly be divided into 3 stages:

  1. Pre-estimation
  2. Estimation
  3. Post-estimaton

At each stage, the goal is to complete a different task (e.g., to clean data, fit a model, test a hypothesis), but the process is sequential — we move through the stages in order (though often many times in one project!)

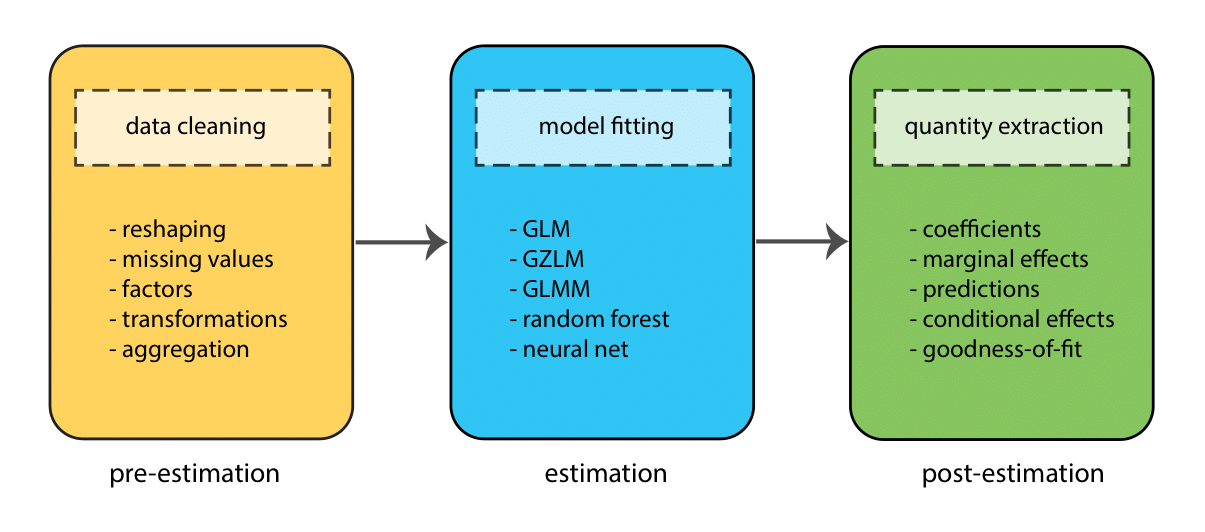
Throughout this workshop we will go through these stages several times as we fit different types of model.

Before fitting a model

GOAL: To learn about the data by creating summaries and visualizations.

The dataset

We have a dataset (states.dta) on a variety of variables for all 50 states. Variables include population, density, energy use, voting tendencies, graduation rates, income, etc.

We’re going to ask the question: does the amount of money spent on education (expense), family income(income), and percentage of students taking SATs (percent) affect the mean SAT score (csat) in a state?

Set working directory

Files are located in the dataSets folder in StataMod. Start by telling Stata where to look for these:

// change directory
cd "~/Desktop/Stata/StataMod"

Use dir to see what is in the directory:

dir
cd dataSets

Load the data

// use the states data set
use dataSets/states.dta

Examine descriptive statistics

// descriptive statistics 
sum expense income percent csat

Visualize the data

// visualize data 
scatter expense income
scatter expense percent

Models with continuous outcomes

GOAL: To learn about the Stata modeling ecosystem by using the regress command to fit ordinary least squares (OLS) models. In particular:

  1. Stata syntax for model specification
  2. Model diagnostics for checking OLS assumptions
  3. Including interaction terms
  4. Including categorical predictors

Fit the model

To fit a model in Stata, we first have to convert our theoretical model into Stata syntax — a symbolic representation of the model:

// model specification
command outcome pred1 pred2 pred3

Note that immediately after the modeling command comes the outcome variable, followed by numerous predictors.

For example, the following model predicts SAT scores based on the amount of money spent on education (expense), family income(income), and percentage of students taking SATs (percent) in a state. Here’s the theoretical model:

\[ SATscores_i = \beta_01 + \beta_1expenditures_i + \beta_2income_i +\beta_3SATpercent_i + \epsilon_i \]

And here’s how we use the regress command to fit this model in Stata:

regress csat expense income percent

OLS assumptions

OLS regression relies on several assumptions, including:

  1. The model includes all relevant variables (i.e., no omitted variable bias).
  2. The model is linear in the parameters (i.e., the coefficients and error term).
  3. The error term has an expected value of zero.
  4. All right-hand-side variables are uncorrelated with the error term.
  5. No right-hand-side variables are a perfect linear function of other RHS variables.
  6. Observations of the error term are uncorrelated with each other.
  7. The error term has constant variance (i.e., homoscedasticity).
  8. (Optional - only needed for inference). The error term is normally distributed.

We can investigate assumptions #7 and #8 by plotting model diagnostics. A simple histogram of the residuals can be informative:

// graph the residual values of csat
predict resid, residual
histogram resid, normal

We can also examine homoscedasticity:

rvfplot, yline(0)

Type -help regress postestimation — for more information about model diagnostics. If assumptions are not met, alter the specification and refit the model.

Interactions

What if we wanted to test an interaction between percent and high?

Option 1: generate product terms by hand:

// generate product of percent and high
gen percenthigh = percent*high 
regress csat expense income percent high percenthigh

Option 2: let Stata do your dirty work:

// use the # sign to represent interactions 
regress csat percent high c.percent#c.high
// same as: regress csat c.percent##c.high

Categorical predictors

For categorical variables, we first need to dummy code. Let’s use region as an example.

Option 1: create dummy codes before fitting regression model:

// create region dummy codes using tab 
tab region, gen(region)

// regress csat on region
regress csat region1 region2 region3

Option 2: let Stata do it for you:

// regress csat on region using fvvarlist syntax
// see `help fvvarlist` for details
regress csat i.region

Exercise 0

Regression with continuous outcomes

Open the datafile, gss.dta.

Fit an OLS regression model to predict general happiness (happy) based on respondent’s sex (sex), marital status (marital), highest year of school completed (educ), and respondent’s income for last year (rincome).

  1. Before running the regression, examine descriptive statistics of the variables and generate a few scatterplots.
##
  1. Run your regression model.
##
  1. Examine the plausibility of the assumptions of normality and homoscedasticity.
##
  1. Add on to the regression equation by generating an interaction term between sex and educ and testing the interaction.
##
Click for Exercise 0 Solution

Open the datafile, gss.dta.

Fit an OLS regression model to predict general happiness (happy) based on respondent’s sex (sex), marital status (marital), highest year of school completed (educ), and respondent’s income for last year (rincome).

  1. Before running the regression, examine descriptive statistics of the variables and generate a few scatterplots.
sum happy educ rincome 
tab sex 
tab marital 

scatter happy rincome
  1. Run your regression model.
regress happy i.sex educ i.marital rincome
  1. Examine the plausibility of the assumptions of normality and homoscedasticity.
hist happy, normal 
rvfplot,yline(0)
  1. Add on to the regression equation by generating an interaction term between sex and educ and testing the interaction.
regress happy i.sex##c.educ i.marital rincome

Models with binary outcomes

GOAL: To learn how to use the logit command to model binary outcomes. In particular:

  1. Run the model to obtain estimates on the log odds scale
  2. Transform model coefficients into odds ratios

The Dataset

Using the states.dta data, we’re going to ask the question: does people per square mile (density), percent HS graduates taking SAT (percent), and per pupil expenditures for primary and secondary school (expense) affect the probability of having an SAT score greater than or equal to 1000 (sat_binary)?

Load the dataset

// use the states data set
use dataSets/states.dta

Recode the outcome variable

Recode the composite SAT score (csat) into two categories: whether a region’s mean SAT score is greater than or equal to 1000, or less than 1000.

gen sat_binary = .
replace sat_binary = 0 if csat < 1000
replace sat_binary = 1 if csat >= 1000

Run summary statistics

tab sat_binary
sum density percent expense

Run the logistic model

Let’s predict the probability of having mean SAT score greater than or equal to 1000 based on density, percent, and expense.

Here’s the theoretical model:

\[ logit(p(SAT1000_i = 1)) = \beta_{0}1 + \beta_1density_i + \beta_2SATpercent_i + \beta_3expenditures_i \]

where \(logit(\cdot)\) is the non-linear link function that relates a linear expression of the predictors to the expectation of the binary response:

\[ logit(p(SAT1000_i = 1)) = ln \left( \frac{p(SAT1000_i = 1)}{1-p(SAT1000_i = 1)} \right) = ln \left( \frac{p(SAT1000_i = 1)}{p(SAT1000_i = 0)} \right) \]

And here’s how we use the logit command to fit this model in Stata:

// logit regression with estimates on the log odds scale 
logit sat_binary density percent expense

// logit regression with estimates on the odds ratio scale 
logit sat_binary density percent expense, or

Exercise 1

Regression with binary outcomes

Use the data file, gss.dta. Examine how age of a respondent (age), highest year of school completed (degree), hours per day watching TV (tvhours), and total family income for last year (income) relate to whether someone uses internet (usenet).

  1. Load the dataset.
##
  1. Run summary statistics, delete subjects who did not provide an answer to the usenet question.
##
Click for Exercise 1 Solution

Use the data file, gss.dta. Examine how age of a respondent (age), highest year of school completed (degree), hours per day watching TV (tvhours), and total family income for last year (income) relate to whether someone uses internet (usenet).

  1. Load the dataset.
use gss.dta, clear
  1. Run summary statistics, delete subjects who did not provide an answer to the usenet question.
tab usenet 
drop if usenet == 9
tab degree 
sum age tvhours income

Exporting & saving results

GOAL: To learn how to store and export Stata models. In particular:

  1. How to store results from models
  2. How to compare models
  3. How to export Stata model output to Excel

Storing results

Stata offers several user-friendly options for storing and viewing regression output from multiple models. First, download the necessary packages:

// install outreg2 package
findit outreg2

Then store the results of some regression models using the estimates command and store option:

// fit two regression models and store the results
regress csat expense income percent high
estimates store Model1
  
regress csat expense income percent high i.region
estimates store Model2

The stored models can be recalled by name using the estimates command and replay option:

// display Model1
estimates replay Model1

Comparing models

The stored models can be compared by name using the estimates command and table option. For a more formal comparison, the lrtest command can be used to perform a likelihhod ratio test:

// compare Model1 and Model2 coefficients
estimates table Model1 Model2

// compare Model1 and Model2 fit 
lrtest Model1 Model2

Exporting to Excel

To avoid human error when transferring coefficients into tables, Excel can be used to format publication-ready tables:

outreg2 [Model1 Model2] using csatprediction.xls, replace

Exercise 2

Exporting & saving results

  1. Fit the logistic model and save it as Model1.
##
  1. Add another predictor (hrs1) in the model and save the new model as Model2 and compare between Model1 and Model2.
##
  1. Save the output of the better fitted model to a word document.
##
Click for Exercise 2 Solution
  1. Fit the logistic model and save it as Model1.
logit usenet age i.degree tvhours income 
est store Model1
  1. Add another predictor (hrs1) in the model and save the new model as Model2 and compare between Model1 and Model2.
logit usenet age i.degree tvhours income hrs1
est store Model2 

lrtest Model1 Model2
  1. Save the better fitted model output to a word document.
logit usenet age i.degree tvhours income hrs1
outreg2 using Mymodel.doc

Obtaining quantities of interest

GOAL: To obtain easy to interpret output from regression models. In particular:

  1. Margins of responses (a.k.a. predictive margins)
  2. Margins of changes of responses (a.k.a. marginal effects)
  3. Graphs of margins

The default summary model output that Stata produces is useful and intuitive for relatively simple models, especially if the outcome is continuous. For more complex models, especially non-linear models or those with interactions, the default output only reports a small subset of information from the model and/or presents results on an unintuitive scale. For such models, it is often easier to interpret margins — specifically, margins of responses or margins of changes in responses. Margins are statistics calculated from predictions of a previously fit model at fixed values of some covariates and averaging over the remaining covariates. Margins answers the question, “What does my model have to say about such-and-such a group or such-and-such a person?”. It answers this question:

  1. Either conditionally –— based on fixed values of covariates (e.g., the mean) -—- or averaged over the observations in the data.
  2. In terms of the response given covariate levels (margins of responses), or any other response you can calculate as a function of your estimated parameters -—- linear responses, probabilities, hazards, survival times, odds ratios, risk differences. (a.k.a. predictive margins, or adjusted predictions, or estimated marginal means, or least-squares means).
  3. In terms of the change in the response for a change in covariate levels (margins of changes in responses). (a.k.a. marginal effects or partial effects).
  4. Providing standard errors, test statistics, and confidence intervals and those statistics can take the covariates as given or adjust for sampling.

To calculate such effects in Stata, we need a flexible way of obtaining quantities of interest from the model. This is generally done using a post-estimation tool. The main post-estimation tool Stata has in its arsenal is the margins command. This is a very flexible tool for producing a variety of quantities of interest from almost all model types that Stata supports. In particular, margins can calculate:

  1. Different types of margins of responses:
    • APM: Average Predictive Margins (average of the responses among actual people in the data)
    • PMM: Predictive Margins at the Means (expected response for a person with average characteristics)
    • PMR: Predictive Margins at Representative values (expected response across a range of covariate values)
  2. Difference types of margins of changes in responses:
    • AME: Average Marginal Effects (average of the changes in responses among actual people in the data)
    • MEM: Marginal Effects at the Means (expected change in response for a person with average characteristics)
    • MER: Marginal Effects at Representative values (expected change in response across a range of covariate values)

The margins command can only be used after you’ve run a regression and acts on the results of the most recent regression command. The marginsplot command can be used to graph any of these margins or comparisons of margins and acts on the results of the most recent margins command.

Margins of responses

GOAL: To learn how to produce margins of responses. In particular:

  1. APM: Average Predictive Margins
  2. PMM: Predictive Margins at the Means
  3. PMR: Predictive Margins at Representative values
  4. Graph margins of responses

The dataset

The case study examples use the nhanesII dataset (Second National Health and Nutrition Examination Survey), which was conducted in the mid to late 1970s. More on the study can be found at https://wwwn.cdc.gov/nchs/nhanes/nhanes2/. Let’s load the data:

use dataSets/nhanesII.dta

Fit a model

We will examine a continuous measure of systolic blood pressure (bpsystol) as a function of a respondent’s age (age), whether they have diabetes (diabetes), and what geographical region they come from (region), using OLS regression.

regress bpsystol age i.diabetes i.region

APM: Average Predictive Margins

If you just type margins by itself, Stata will calculate the predicted value of the model outcome (bpsystol) for each observation in the data, then report the mean value of those predictions.

margins

If margins is followed by a categorical variable, for example, region, Stata first identifies all the levels of the categorical variable. Then, it calculates what the mean predicted value of the model outcome (bpsystol) would be if all observations had that value for region. All other variables are left unchanged.

// margins for dummy variable 
margins diabetes

// margins for multi-level categorical variable 
margins region

PMM: Predictive Margins at the Means

By default, margins reports the average of the predictions for each person (i.e., observation) in the data. This is the average response among the actual people in the data. But we can also get margins to report the prediction at the average of the covariates by using the atmeans option. This represents the expected response of a person with average characteristics.

// margins for dummy variable 
margins diabetes, atmeans

PMR: Predictive Margins at Representative values

For continuous variables, margins cannot look at all possible values, but we can specify which values we want to examine with the at option:

margins, at(age = (50 80))

The previous step calculates the mean predicted value of the model outcome (bpsystol) with age set to 50, and then again with age set to 80. We can also add more values by listing the numbers we want in a numlist:

// predicted values for ages 50 to 80 in 5 year increments
margins, at(age=(50(5)80))

Graph margins of responses

The previous step calculates the mean predicted value of bpsystol with age set to 50, 55, 60, 65, 70, 75, and 80. We can now use marginsplot to graph the results.

marginsplot

Exercise 3

Margins of responses

Open the datafile gss.dta.

  1. Fit an OLS regression model to predict general happiness (happy) based on respondent’s sex (sex), marital status (marital), highest year of school completed (educ), and respondent’s income for last year (rincome). Obtain average predictive margins for happy.
##
  1. Obtain predictive margins of sex and marital.
##
  1. Obtain predictive margins of rincome from 10000 to 30000, with an interval of 5000.
##
  1. Create a marginsplot and interpret the results.
##
Click for Exercise 3 Solution

Open the datafile gss.dta

  1. Fit an OLS regression model to predict general happiness (happy) based on respondent’s sex (sex), marital status (marital), highest year of school completed (educ), and respondent’s income for last year (rincome). Obtain average predictive margins for happy.
regress happy i.sex educ i.marital rincome
margins
  1. Obtain predictive margins of sex and marital.
margins, sex 
margins, marital
  1. Obtain predictive margins of rincome from 10000 to 30000, with an interval of 5000.
margins, at(rincome=(10000(5000)30000))
  1. Create a marginsplot and interpret the results.
marginsplot

Margins of changes in responses

GOAL: To learn how to produce margins of changes in responses. In particular:

  1. AME: Average Marginal Effects
  2. MEM: Marginal Effects at the Means
  3. MER: Marginal Effects at Representative values
  4. Graph margins of changes in responses

The dataset

We will be using the same dataset as the previous example: the Second National Health and Nutrition Examination Survey (NHANES II). Let’s load the data:

use dataSets/nhanesII.dta

Fit a model

We will predict the probability of someone having diabetes (diabetes), as a function of race (black), sex (female), and age (age), using logistic regression.

logit diabetes black female age, nolog

AME: Average Marginal Effects

We can first obtain the Average Predictive Margins of race (black) and sex (female). Then, we can use the dydx command to estimate changes in the response when the levels of race and sex change. Since, by default, these changes are averaged over each person in the dataset, we obtain Average Marginal Effects. As the current model is logistic, margins automatically back-transforms the APMs and AMEs from the estimation scale (i.e., the log odds scale) to the response scale (i.e., the probability scale).

// obtain Average Predictive Margins 
margins black female 

// calculate the average of all the marginal effects 
margins, dydx(black female)

MEM: Marginal Effects at the Mean

By default, margins with the dydx command reports the average of the changes in the probability of the response among actual people in the data. But we can also get margins to report the expected change in the probability of the response for a person with average characteristics by using the atmeans option.

// obtain Predictive Margins at the Means
margins black female, atmeans

// calculate marginal effects with all other covariates fixed at their sample means 
margins, dydx(black female) atmeans

MER: Marginal Effects at Representative values

For continuous variables, margins needs us to specify which values we want to examine using the at option. We can calculate the change in the probability of the model outcome (diabetes) when levels of race (black) and sex (female) change, across a range of values for age by supplying a list of numbers to a numlist:

// obtain Predictive Margins at Representative values
// choose range of values for one or more variables
// note: the `vsquish` option omits vertical white space between results
margins black, at(age=(20 30 40 50 60 70)) vsquish 

// calculate marginal effects across that range 
margins, dydx(black female) at(age=(20 30 40 50 60 70)) vsquish

Graph margins of changes in responses

The previous step calculates the average change in the predicted probability of diabetes, when levels of race (black) and sex (female) change, with age set to 20, 30, 40, 50, 60, and 70. We can now use marginsplot to graph the results.

marginsplot

Exercise 4

Margins of changes in responses

Open the datafile gss.dta.

  1. Fit a logistic model to examine how whether someone uses internet (usenet) is related to age of the respondent (age), highest year of school completed (degree), hours per day watching TV (tvhours), and total family income for last year (income). Obtain Average Predictive Margins and Average Marginal Effects for degree.
##
  1. Obtain Predictive Margins of degree at Representative values of tvhours from 0 to 10 hours, on a 1 hour interval. Examine how the marginal effect of degree differs across the range of tvhours (i.e., obtain Marginal Effects at Representative values).
##
  1. Create a marginsplot for the marginal effects from #2.
##
Click for Exercise 4 Solution

Open the datafile gss.dta.

  1. Fit a logistic model to examine how whether someone uses internet (usenet) is related to age of the respondent (age), highest year of school completed (degree), hours per day watching TV (tvhours), and total family income for last year (income). Obtain Average Predictive Margins and Average Marginal Effects for degree.
logit usenet age i.degree tvhours income 

margins degree
margins, dydx(degree)
  1. Obtain Predictive Margins of degree at Representative values of tvhours from 0 to 10 hours, on a 1 hour interval. Examine how the marginal effect of degree differs across the range of tvhours (i.e., obtain Marginal Effects at Representative values).
margins degree, at(tvhours=(0 1 2 3 4 5 6 7 8 9 10) vsquish 
margins, dydx(degree) at(tvhours=(0 1 2 3 4 5 6 7 8 9 10)) vsquish
  1. Create a marginsplot for the marginal effects from #2.
marginsplot

Wrap-up

Feedback

These workshops are a work in progress, please provide any feedback to: