Compute Model Dependence Bounds

modelDependence() computes model dependence bounds for a single dataset using either the extreme bounds procedure or Athey-Imbens procedure. The width of the bounds indicates the degree of model dependence present in the dataset. Wide bounds imply that treatment effects could vary greatly depending on the outcome model used and therefore depend heavily on it.

modelDependence(base.form = NULL, data, treatment,
                outcome, covariates, weights = NULL,
                method = c("extreme-bounds", "athey-imbens"),
                model.dependence.ests = 101,
                specifications = NULL, cutpoints = NULL,
                cutpoint.method = c("mean", "median", "segmented"),
                verbose = TRUE, seed = NULL)

# S3 method for modelDependenceBounds
plot(x, ...)

# S3 method for modelDependenceBounds
print(x, ...)

Arguments

base.form: a formula relating the outcome to the treatment and covariates, e.g., Y ~ A + X1 + X2 + ... where Y represents the outcome variable, A the treatment variable, and X1 and X2 the covariates. This should correspond to the "default" or originally intended outcome model whose sensitivity is being assessed. If omitted, will just use a simple regression of the outcome on the treatment.
data: a data frame containing the variables named in base.form, treatment, outcome, and covariates.
treatment: the name of the treatment variable. If missing and base.form is specified and only has one right-hand side variable, that variable will be considered the treatment.
outcome: the name of the outcome variable. Ignored if base.form is supplied and required otherwise.
covariates: a character vector containing the names of the covariates over which model dependence is to be assessed. Can also be a one-sided formula with the covariates on the right-hand side. If omitted, all variables in base.form that are not the treatment or outcome will be considered covariates.
weights: an optional vector of weights (e.g., matching weights) to be included in the fitted models.
method: the method of computing model dependence bounds. Can be one of "extreme-bounds" or "athey-imbens" for the extreme bounds or Athey-Imbens procedures, respectively. Abbreviations allowed. Default is extreme bounds. See Details.
model.dependence.ests: when method = "extreme-bounds", the number of different model specifications to use. Higher numbers give more accurate bounds but take longer. Exactly one of model.dependence.ests or specifications must be supplied.
specifications: when method = "extreme-bounds", a list of formulas containing all the model specifications to consider in computing the extreme bounds. If omitted, these will be randomly generated using up to third degree polynomials and two-way interactions between covariates. Exactly one of model.dependence.ests or specifications must be supplied.
cutpoints: when method = "athey-imbens", a named list of the cutpoints for each covariate that has more than two unique values. A cutpoint of NA means the unique values of the variable will be used. For any covariates without cutpoints specified, the cutpoints will computed using the method supplied to cutpoint.method.
cutpoint.method: when method = "athey-imbens", the name of the method to create cutpoints for covariates without entries in cutpoints. Options include "mean" (the default) to use the covariate mean as the cutpoint, "median" to use the covariate median as the cutpoint, and "segmented" to estimate the cutpoints with segmented (piecewise) regression. Abbreviations allowed.
verbose: logical; whether to print additional information about the procedure.
seed: the seed for the random number generator. If NULL, the current seed is used.
x: a modelDependenceBounds object, the output of a call to modelDependence().
...: for print.modelDependenceBounds, further arguments passed to print(). Ignored otherwise.

Details

The simplest way to estimate the model dependence bounds is to supply base.form with the treatment and covariates on the right hand side and treatment supplied.

The extreme bounds procedure (Leamer, 1983) works by fitting many different models of various functional forms with many combinations of the covariates. When specifications is not supplied, these models are randomly generated by appending to the model in base.form sets of squares, cubes, and two-way interactions of the covariates with model.dependence.ests controlling how many such models are estimated. More is always better but will take longer. The 5th and 95th percentiles of the treatment effects from all the specifications are used as the model dependence bounds.

The Athey-Imbens procedure (Athey & Imbens, 2015) works by splitting covariates at points determined by cutpoints or cutpoint.method, fitting the base.form model within each subset, averaging the two effect estimates, and computing the standard deviation of the resulting effect estimates. The base treatment effect estimate (fit in the full sample) minus and plus this standard deviation are used as the model dependence bounds. cutpoints can be supplied or estimated for each covariate. For covariates with exactly two unique values, the data will be split according to those values. For covariates with more than two values, if a cutpoint is supplied, it will be used to split the dataset; otherwise, a cutpoint will be estimated as the mean or median of the covariate or using segmented regression as implemented in segmented::segmented() depending on the argument to cutpoint.method.

It is important to consider the interpretation of base.form. If there is no confounding by the covariates (e.g., because of the result of a randomized experiment or successful matching), base.form can specified simply as Y ~ A, with model dependence referring to all the possible adjustment sets and their functional forms. If there is confounding and base.form is specified as Y ~ A (or with only a subset of the confounding covariates included in the model), then model dependence concerns different adjustment sets, and therefore muddles dependence on model specification and covariate choice, which is undesirable. base.form should therefore contain all the covariates required to eliminate confounding, with the model dependence referring to the possible additional terms that could be added to the model to change its functional form. Put simply, the adjustment set should always be in base.form, but after randomization or successful matching the adjustment set might be empty.

Value

A modelDependenceBounds object, which is numeric vector with the lower and upper model dependence bounds and attributes concerning the fit. The attribute "method" will contain the method supplied to method. The attribute base.est will contain the effect estimated using base.form with no modification. The attribute "estimates" will contain the effect estimates used in computing the bounds. For the extreme bounds procedure, the attribute "sepcifications" contains a list of the model specifications used, each as a string representing the model formula. This can be supplied to future calls to modelDependence() or estimateEffects(). For the Athey-Imbens procedure, the attribute "sigma" contains the standard deviation of the effect estimates that, when added to and subtracted from the estimate resulting from the model specified in base.form, forms the bounds.

The print() method displays the bounds as well as their difference. Note that the difference is not actually stored in the modelDependenceBounds object but can be computed using diff().

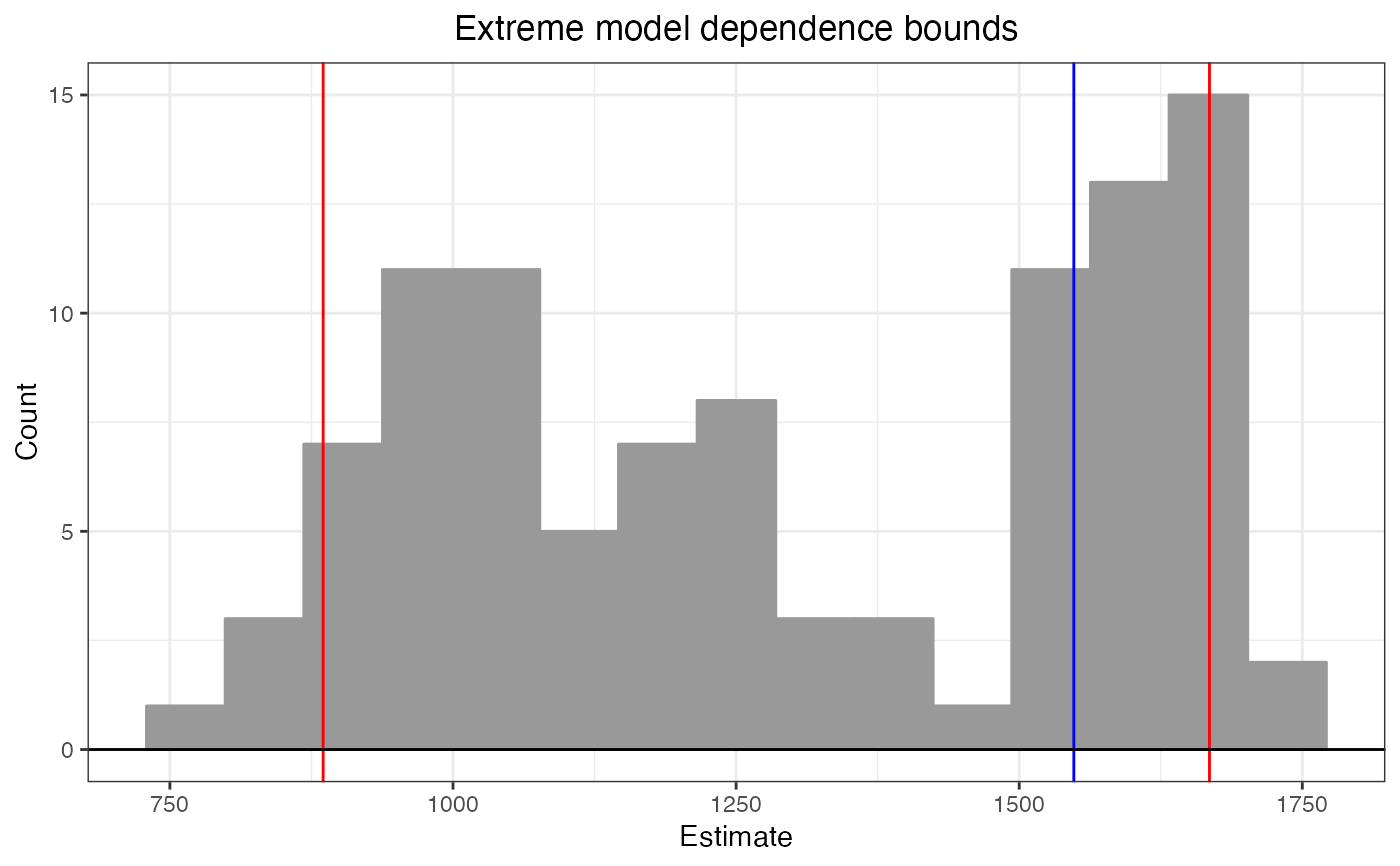
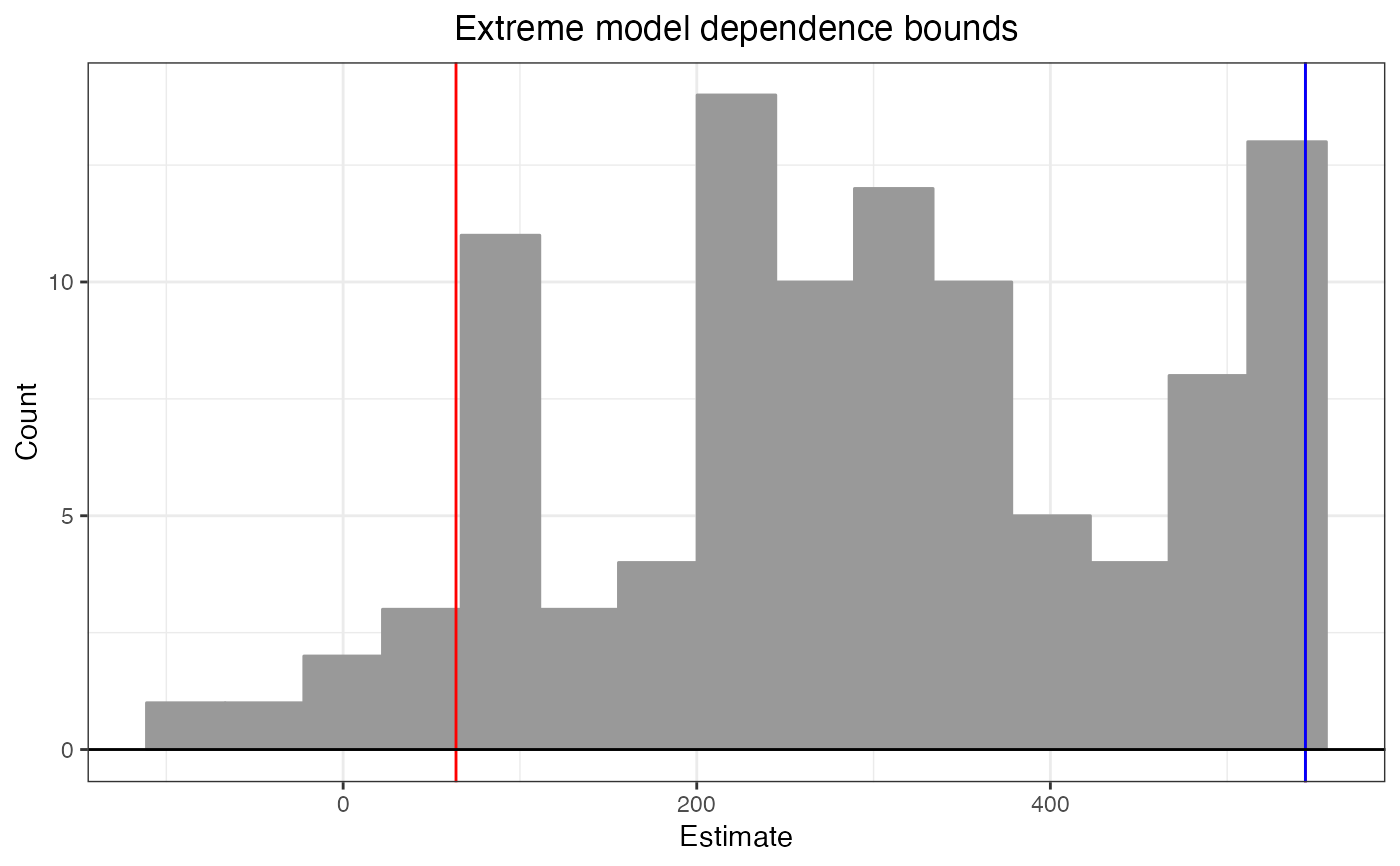
The plot() method displays a histogram of the effect estimates when method = "extreme-bounds" and a dot plot of the estimates when method = "athey-imbens". Red vertical lines indicate the reported bounds, and the blue vertical line indicates the base estimate. The resulting object is a ggplot object that can be further manipulated using ggplot2 functionality.

References

Athey, S., & Imbens, G. (2015). A measure of robustness to misspecification. American Economic Review, 105(5), 476-80.

Leamer, E. E. (1983). Let's take the con out of econometrics. The American Economic Review, 73(1), 31-43.

Examples

library(MatchIt)
data("lalonde", package = "MatchIt")

#Model dependence prior to matching
b1 <- modelDependence(re78 ~ treat + age + educ + married +
                        race + nodegree + re74 + re75,
                      data = lalonde, treatment = "treat",
                      method = "extreme-bounds", seed = 12345)
b1 # diff = 823.8418
#> Extreme model dependence bounds: 
#>     lower     upper      diff 
#>  885.3360 1668.0174  782.6814 
plot(b1)


#Model dependence after matching
m.out <- matchit(treat ~ age + educ + married + race +
                   nodegree + re74 + re75, data = lalonde,
                 distance = "mahalanobis", replace = TRUE)

b2 <- modelDependence(re78 ~ treat + age + educ + married +
                        race + nodegree + re74 + re75,
                      data = lalonde, treatment = "treat",
                      method = "extreme-bounds", seed = 12345,
                      weights = m.out$weights)
b2 # diff = 684.6681
#> Extreme model dependence bounds: 
#>     lower     upper      diff 
#>  63.83596 544.24800 480.41204 
plot(b2)


#Athey-Imbens bounds using various cutpoints
#  Here we use cutpoints of 100 for re74 and re75 and split
#  other covariates at their means
b3 <- modelDependence(re78 ~ treat + age + educ + married +
                        race + nodegree + re74 + re75,
                      data = lalonde, treatment = "treat",
                      method = "athey-imbens",
                      cutpoints = list(re74 = 100, re75 = 100),
                      cutpoint.method = "mean")
b3
#> Athey-Imbens model dependence bounds: 
#>    lower    upper     diff 
#> 1043.574 2052.914 1009.340 
plot(b3)

Arguments

Details

Value

References

See also

Examples